

They are the parameters of the system and the system’s properties depend on them. While t does not appear in the equations, sigma, beta & rho do. For this particular system we could actually build a function that does not take the parameter t but I include it because it can be useful if you want to add discontinuities that depend on t. So why can we ignore t here? The answer is that our numerical integrator will keep track of t for us. The amount of change certainly depends on the amount of time. The fact that the variable t does not show up in any of these equations is a common point of confusion. Python nonlinear systems of equations using fsolve - YouTube 0:00 16:29 Python nonlinear systems of equations using fsolve 1.39K subscribers Subscribe 9.7K views 3.
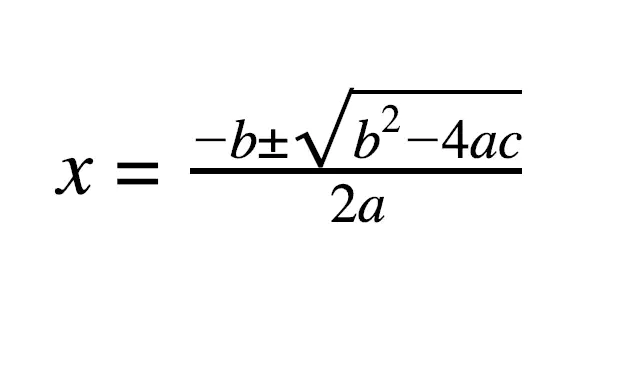
#SOLVING THREE EQUATION SYSTEMS WITH PYTHON FULL#
Computes the exact solution, x, of the well-determined, i.e., full rank, linear matrix. This is followed by the three differential equations that described the dynamic changes of the state variables. Solve a linear matrix equation, or system of linear scalar equations. A value of each of the unknown or variable satisfies both the equation simultaneously. Inside the lorenz function, the first thing we do is to unpack the state into the three state variables. Methods of Solving a System of Equations in Two Variables. Our state object has to be a sequence with an order that reflects this. Python nonlinear systems of equations using fsolve 1.43K subscribers Subscribe 10K views 3 years ago Python, solving systems of nonlinear equations using fsolve. Most importantly, the first parameter must be the state of the system.The state of the Lorenz system is defined by three variables: x, y, z. This function needs a specific call signature ( lorenz(state, t, sigma, beta, rho)) because we will later pass it to odeint which expects specific parameters in specific places. It consists of three differential equations that we fit into one function called lorenz. After that we define the system of differential equations that defines our Lorenz system. The forcing function is similar to the Dirac delta distribution in this simulation.
#SOLVING THREE EQUATION SYSTEMS WITH PYTHON CODE#
Matplotlib will be used to plot the result of our simulation. Gist 3 shows the Python code with the ODEs implemented as a Numpy array. Of course we need NumPy and odeint is imported from scipy.integrat.


 0 kommentar(er)
0 kommentar(er)
